Решение: Космический корабль на скорости 10 км/с попадает в неподвижное облако

Условие задачи:

Космический корабль на скорости 10 км/с попадает в неподвижное облако микрометеоритов с плотностью вещества 20 мг/м³. На сколько должна возрасти сила тяги двигателя, чтобы скорость корабля не изменилась, если его лобовое поперечное сечение 50 м². Удар микрометеоритов об обшивку корабля считать неупругим.

Задача №2.10.33 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$\upsilon=10$ км/с, $\rho=20$ мг/м³, $S=50$ м², $F-?$

Решение задачи:

Если скорость корабля при неупругом ударе с микрометеоритами не будет изменяться, значит сила тяги двигателя возросла на величину $F$ , которую можно определить из второго закона Ньютона, записанного в общем виде:

$F = \frac{{\Delta p}}{{\Delta t}}\;\;\;\;(1)$

Здесь $\Delta p$ — это изменение импульса микрометеоритов вследствие удара об обшивку корабля, которая очевидно равна:

$\Delta p = m\upsilon \;\;\;\;(2)$

Нам нужно определить массу микрометеоритов $m$ , с которыми сталкивается в единицу времени $\Delta t$ корабль. Эту массу очень легко определить через плотность $\rho$ по такой формуле:

$m = \rho \Delta V\;\;\;\;(3)$

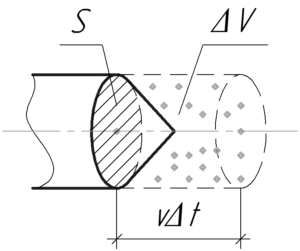
Тут $\Delta V$ — это тот объем пространства с метеоритами, который преодолевает корабль за время $\Delta t$ . Скорость корабля равна $\upsilon$ , а площадь лобового сечения $S$ , поэтому вполне очевидно, что:

$\Delta V = S\upsilon \Delta t\;\;\;\;(4)$

Подставим (4) в (3), далее полученное в (2), а полученное после этого в (1):

$F = \rho S{\upsilon ^2}$

Задача решена в общем виде. Переведем плотность облака и скорость корабля в систему СИ, а уже потом вычислим ответ:

$20\; мг/м^3 = \frac{{20}}{{{{10}^3}}}\; г/м^3 = \frac{{20}}{{{{10}^6}}}\; кг/м^3 = 2 \cdot {10^{ — 5}}\; кг/м^3$

$10\; км/с = 10 \cdot {10^3}\; м/с = {10^4}\; м/с$

$F = 2 \cdot {10^{ — 5}} \cdot 50 \cdot {10^8} = {10^5}\; Н = 0,1\; МН$