Условие задачи:
Камень, подвешенный к потолку на веревке, движется в горизонтальной плоскости по окружности, отстоящей от потолка на расстояние 90 см. Найти период обращения камня.
Задача №2.4.14 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(h=90\) см, \(T-?\)
Решение задачи:
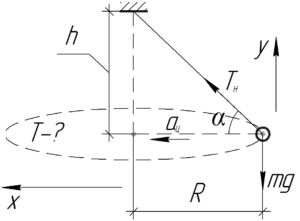 На камень действуют две силы: это сила тяжести \(mg\) и сила натяжения нити \(T_н\) (индекс добавлен для того, чтобы не путать с периодом \(T\)). Оси координат и другие геометрические параметры вы можете видеть на схеме.
На камень действуют две силы: это сила тяжести \(mg\) и сила натяжения нити \(T_н\) (индекс добавлен для того, чтобы не путать с периодом \(T\)). Оси координат и другие геометрические параметры вы можете видеть на схеме.
Тело неподвижно вдоль оси \(y\), применим первый закон Ньютона в проекции на эту ось:
\[{T_н} \cdot \sin \alpha = mg\;\;\;\;(1)\]
В горизонтальной плоскости камень описывает окружность некоторого радиуса \(R\). Запишем второй закон Ньютона в проекции на ось \(x\):
\[{T_н} \cdot \cos \alpha = m{a_ц}\;\;\;\;(2)\]
Запишем формулу определения центростремительного ускорения \(a_ц\) через угловую скорость вращения \(\omega\) и формулу связи последней с периодом обращения \(T\):
\[{a_ц} = {\omega ^2}R\]
\[\omega = \frac{{2\pi }}{T}\]
Таким образом, ускорение камня можно найти по формуле:
\[{a_ц} = \frac{{4{\pi ^2}}}{{{T^2}}}R\]
Равенство (2) примет вид:
\[{T_н} \cdot \cos \alpha = \frac{{4{\pi ^2}}}{{{T^2}}}mR\]
Поделим равенство (1) на последнее, тогда:
\[tg\alpha = \frac{{g{T^2}}}{{4{\pi ^2}R}}\]
Выразим нужный нам период обращения \(T\):
\[{T^2} = \frac{{4{\pi ^2}R \cdot tg\alpha }}{g}\]
\[T = 2\pi \sqrt {\frac{{R \cdot tg\alpha }}{g}} \;\;\;\;(3)\]
Глядя на схему видно, что тангенс угла \(\alpha\) равен:
\[tg\alpha = \frac{h}{R}\]
Если подставить это выражение в формулу (3), получим решение задачи в общем виде:
\[T = 2\pi \sqrt {\frac{h}{g}} \]
Переведем расстояние \(h\) в систему СИ:
\[90\; см = \frac{{90}}{{100}}\; м = 0,9\; м\]
Теперь считаем ответ:
\[T = 2 \cdot 3,14 \cdot \sqrt {\frac{{0,9}}{{10}}} = 1,9\; с\]
Ответ: 1,9 с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.4.13 Шоссе имеет вираж с уклоном 10 градусов при радиусе закругления дороги в 100 м
2.4.15 В желобе, наклоненном под углом 30 градусов к горизонту и вращающемся с частотой
2.4.16 Гирька массой 0,1 кг, привязанная легкой нерастяжимой нитью, описывает окружность

