Условие задачи:
Камень бросили под углом 60° к горизонту со скоростью 15 м/с. Найдите кинетическую энергию камня спустя 1 с после начала движения. Масса камня 0,1 кг.
Задача №2.8.29 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\alpha=60^\circ\), \(\upsilon_0=15\) м/с, \(t=1\) с, \(m=0,1\) кг, \(E_к-?\)
Решение задачи:
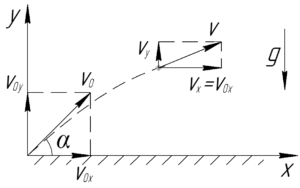 Из кинематики известно, что при движении тела под углом к горизонту проекции скорости тела на оси координат определяются следующим образом:
Из кинематики известно, что при движении тела под углом к горизонту проекции скорости тела на оси координат определяются следующим образом:
\[\left\{ \begin{gathered}
ox:{\upsilon _x} = {\upsilon _0}\cos \alpha \hfill \\
oy:{\upsilon _y} = {\upsilon _0}\sin \alpha — gt \hfill \\
\end{gathered} \right.\]
Модуль скорости тела можно найти по формуле (теорема Пифагора):
\[\upsilon = \sqrt {\upsilon _x^2 + \upsilon _y^2} \]
Тогда понятно, что кинетическую энергию камня легко посчитать по следующей формуле:
\[E_к = \frac{{m{\upsilon ^2}}}{2}\]
\[E_к = \frac{{m\left( {\upsilon _x^2 + \upsilon _y^2} \right)}}{2}\]
Интересно, что так как проекция скорости на ось \(y\) фигурирует в формуле в квадрате, то нас не интересует куда в данный момент движется тело, так как возведение в квадрат уничтожит отрицательный знак.
Подставляя выражения из системы в последнюю формулу, получим решение задачи в общем виде.
\[E_к = \frac{{m\left( {\upsilon _0^2{{\cos }^2}\alpha + \upsilon _0^2{{\sin }^2}\alpha — 2{\upsilon _0}gt\sin \alpha + {g^2}{t^2}} \right)}}{2}\]
\[E_к = \frac{{m\left( {\upsilon _0^2 — 2{\upsilon _0}gt\sin \alpha + {g^2}{t^2}} \right)}}{2}\]
Посчитаем ответ к задаче:
\[E_к = \frac{{0,1\left( {{{15}^2} — 2 \cdot 15 \cdot 10 \cdot 1 \cdot \sin 60^\circ + {{10}^2} \cdot {1^2}} \right)}}{2} = 3,26\; Дж\]
Ответ: 3,26 Дж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.8.28 Какую работу надо совершить, чтобы поставить однородный куб массой 10 кг
2.8.30 На нити длиной 1 м подвешено тело массой 1 кг. На какой максимальный угол
2.8.31 Пуля, летящая горизонтально со скоростью 400 м/с, попадает в ящик, лежащий
Можно ли решить через закон сохранения энергии?
kE(0)=kE(1)+pE(1)
kE(1)=kE(0)-pE(1)
kE(1)=mv(0)^2 /2 — mg(tV(0)cosa-gt^2 /2)