Условие задачи:
Камень брошен под углом 60° к горизонту. Как соотносятся между собой начальная кинетическая энергия \(T_1\) камня с его кинетической энергией \(T_2\) в верхней точке траектории?
Задача №2.7.55 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\alpha=60^\circ\), \(\frac{T_1}{T_2}-?\)
Решение задачи:
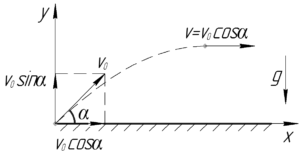 Так как в верхней точке траектории вертикальная составляющая скорости отсутствует, то скорость \(\upsilon\) в этой точке связна с начальной скоростью \(\upsilon_0\) камня следующий соотношением:
Так как в верхней точке траектории вертикальная составляющая скорости отсутствует, то скорость \(\upsilon\) в этой точке связна с начальной скоростью \(\upsilon_0\) камня следующий соотношением:
\[\upsilon = {\upsilon _0} \cdot \cos \alpha \]
Кинетическая энергия камня в момент броска и в верхней точке соответственно равны:
\[\left\{ \begin{gathered}
{T_1} = \frac{{m\upsilon _0^2}}{2} \hfill \\
{T_2} = \frac{{m{\upsilon ^2}}}{2} = \frac{{m\upsilon _0^2{{\cos }^2}\alpha }}{2} \hfill \\
\end{gathered} \right.\]
Искомое соотношение равно:
\[\frac{{{T_1}}}{{{T_2}}} = \frac{1}{{{{\cos }^2}\alpha }}\]
Численно отношение равно:
\[\frac{{{T_1}}}{{{T_2}}} = \frac{1}{{{{\cos }^2}60^\circ }} = 4\]
Ответ: 4.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.7.54 Чему равна кинетическая энергия тела массы 0,2 кг, брошенного вертикально вверх
2.7.56 Тело брошено вертикально вверх со скоростью 30 м/с. Если принять потенциальную
2.7.57 Шарик, подвешенный на нити, качается в вертикальной плоскости так, что его ускорения