Условие задачи:
Какую скорость приобретает ракета массой 2 кг, если продукты горения массой 400 г вылетают из нее со скоростью 800 м/с?
Задача №2.8.5 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(M=2\) кг, \(m=400\) г, \(\upsilon=800\) м/с, \(u-?\)
Решение задачи:
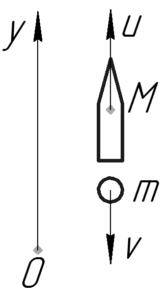Из условия видно, что ракета маленькая, а значит процесс горения её топлива будет настолько быстрым, что никакие внешние силы не успеют за время горения изменить импульс ракеты на значительную величину. Значит справедлив закон сохранения импульса, запишем его в проекции на ось \(y\):
\[0 = Mu – m\upsilon \]
Выразим отсюда искомую скорость ракеты \(u\):
\[u = \frac{{m\upsilon }}{M}\]
Переведем массу продуктов горения в системы СИ:
\[400\; г = \frac{{400}}{{1000}}\; кг = 0,4\; кг\]
Осталось только посчитать ответ.
\[u = \frac{{0,4 \cdot 800}}{2} = 160\; м/с = 576\; км/ч\]
Ответ: 576 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.8.4 Тело находится на краю горизонтальной плоскости. Затем этот край плоскости
2.8.6 Тело массой 2 кг падает с высоты 10 м и углубляется в песок на глубину 0,5 м
2.8.7 Брусок массой 1 кг первоначально покоился на вершине наклонной плоскости
Подскажите,пожалуйста,правильно вычислена высота?
На какое расстояние удалится от поверхности Земли ракета, выпущенная со скоростью 9 км/с ? ( 9 км/сек = 32 400 км/час)
Задача из сборника по решению задач. Автор Р.А. Гладкова, Москва, 1975 год, стр. 100.
Найдём потенциальную энергию такой системы тел. При перемещении тела m из точки R1 в точку R2 будет совершена работа, равная:
A1,2 = (GMm / R2ср) • (R2 — R1).
Существует два средних значения: среднее арифметическое и среднее геометрическое. При малой разности обеих величин различие между средними оказывается намного меньшим, чем различие между величинами. Поэтому мы можем заменить на произведение R1R2. Тогда
A1,2 = (GMm / R2) — (GMm / R1).
Поскольку работа есть разность потенциальных энергий, взятая с обратным знаком, ясно, что
U= -GMm / R.
По закону сохранения энергии:
mv2/2 − GmM / R = −GmM / (R + h),
v2/2 = GM (1/R − 1/(R + h)) = GMh / (R2 + Rh),
h = v2R2 / (2GM − v2R).
Я ошибки не вижу
Здравствуйте,
в некоторых задачах “с подвохом” учитывается масса ракеты, как сумма масс корпуса и топлива. Я почему-то начал именно так и решать, и в результате поделил на 1,6.
Есть какой-то секрет, как такие задачи различать?
На экзаменах и олимпиадах в условии должно быть ясно написано, учитывается ли в массе ракеты ещё и масса топлива, если конечно это не подвох задачи (что бывает на олимпиадах). Но подвох задач очень редко заключается в том, чтобы угадать мысли автора задачи (или что он имеет ввиду под массой ракеты).
Поэтому какого-то секрета я не знаю.
Думаю, что если в условии не сказано явно, что “масса ракеты с топливом равна…”, то следует решать как показано здесь, иначе – как решали Вы.
А можно к этой задаче еще решить вопрос *На какую высоту поднимется ракета?*
Легко:
u^2 = 2*g*H
H=u^2/(2*g)
H=160^2/(2*10)=1280 м
С какой скоростью взлетит модель ракеты, для которой соотно- шение масс ракеты и топлива равно 1:6? Скорость газов в двигателе достигает 8 м/с. На какую высоту поднимется ракета? Можете помочь с этой задачей ?