Условие задачи:
Какую работу надо совершить, чтобы растянуть пружину с жесткостью 40 кН/м на 0,5 см?
Задача №2.7.1 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(k=40\) кН/м, \(x=0,5\) см, \(A-?\)
Решение задачи:
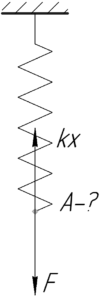Работу \(A\) внешней силы по растяжению пружины на величину \(x\) из недеформированного состояния следует искать по следующей формуле:
\[A = \frac{{k{x^2}}}{2}\]
Переведем величину деформации \(x\) в систему СИ:
\[0,5\;см = \frac{{0,5}}{{100}}\;м = 0,005\;м\]
\[A = \frac{{40 \cdot {{10}^3} \cdot {{0,005}^2}}}{2} = 0,5\;Дж = 500\;мДж\]
Ответ: 500 мДж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.6.15 Деревянный брусок массы 2 кг тянут равномерно по горизонтальной доске с помощью
2.7.2 Какую работу совершает постоянная сила по перемещению на 5 м тела массой 3 кг
2.7.3 Определить работу, необходимую для поднятия груза массой 3 кг на высоту 10 м
А разве формула работы деформированной пружины не A=kx(1)^2/2-kx(2)^2/2?
И если x1 = 0, то работа же получается отрицательной, или я что-т путаю…
Вы написали формулу для определения работы силы упругости пружины \(A_{упр}\), а в задаче требуют найти работу внешней силы по растяжению пружины \(A_{вн}\). Они связаны таким соотношением:\[{A_{вн}} = – {A_{упр}}\]