Условие задачи:
Какую работу должен совершить двигатель, чтобы разогнать по горизонтальной поверхности первоначально неподвижный самосвал массой 3 т до скорости 36 км/ч? Потерями на трение пренебречь.
Задача №2.7.23 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=3\) т, \(\upsilon=36\) км/ч, \(A-?\)
Решение задачи:
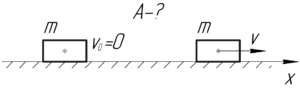 Применим теорему об изменении кинетической энергии. Согласно этой теореме работа двигателя равна изменению кинетической энергии самосвала. Так как самосвал изначально покоился, то аналитическая запись теоремы имеет такой вид:
Применим теорему об изменении кинетической энергии. Согласно этой теореме работа двигателя равна изменению кинетической энергии самосвала. Так как самосвал изначально покоился, то аналитическая запись теоремы имеет такой вид:
\[A = \frac{{m{\upsilon ^2}}}{2}\]
Массу самосвала представим в килограммах, а его конечную скорость — в метрах в секунду.
\[3\;т = 3000\;кг\]
\[36\;км/ч = \frac{{36 \cdot 1000}}{{1 \cdot 3600}}\;м/с = 10\;м/с\]
Произведем расчет ответа:
\[A = \frac{{3000 \cdot {{10}^2}}}{2} = 150000\;Дж = 150\;кДж\]
Ответ: 150 кДж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.7.22 Какая работа совершается внешней силой при поднятии тела массой 5 кг на высоту
2.7.24 Какую работу надо совершить, чтобы поднять груз массой 30 кг на высоту 10 м
2.7.25 Какую работу надо совершить, чтобы поднять груз массой 3000 кг на высоту 10 м