Условие задачи:
Какая доля кинетической энергии перейдет в теплоту при неупругом столкновении двух одинаковых тел, движущихся до удара с равными по модулю скоростями под прямым углом друг к другу?
Задача №2.10.29 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m\), \(\alpha=90^\circ\), \(\frac{Q}{E}-?\)
Решение задачи:
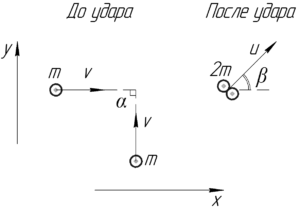 Начальная суммарная кинетическая энергия двух тел равна:
Начальная суммарная кинетическая энергия двух тел равна:
\[E = \frac{{2m{\upsilon ^2}}}{2} = m{\upsilon ^2}\;\;\;\;(1)\]
Запишем закон сохранения импульса в проекции на ось \(x\) и \(y\):
\[\left\{ \begin{gathered}
ox:m\upsilon = 2mu \cdot \cos \beta \hfill \\
oy:m\upsilon = 2mu \cdot \sin \beta \hfill \\
\end{gathered} \right.\]
Поделим нижнее равенство на верхнее, тогда:
\[\operatorname{tg} \beta = 1\]
\[\beta = 45^\circ \]
Из первого равенства системы выразим скорость тел \(u\) после удара:
\[u = \frac{{m\upsilon }}{{2m \cdot \cos \beta }}\]
Так как \(\beta = 45^\circ\), то:
\[u = \frac{\upsilon }{{2\cos 45^\circ }} = \frac{\upsilon }{{\sqrt 2 }}\]
Теперь применим закон сохранения энергии, учитывая, что удар был абсолютно неупругий, и часть энергии перешла в теплоту:
\[\frac{{m{\upsilon ^2}}}{2} + \frac{{m{\upsilon ^2}}}{2} = \frac{{2m{u^2}}}{2} + Q\]
Поскольку мы уже определили, что \(u = \frac{\upsilon }{{\sqrt 2 }}\), то:
\[\frac{{m{\upsilon ^2}}}{2} + \frac{{m{\upsilon ^2}}}{2} = \frac{{2m{\upsilon ^2}}}{{2 \cdot 2}} + Q\]
\[Q = \frac{{m{\upsilon ^2}}}{2}\]
Учитывая (1), найдем искомое отношение \(\frac{Q}{E}\):
\[\frac{Q}{E} = \frac{{m{\upsilon ^2} \cdot 2}}{{2 \cdot 2m{\upsilon ^2}}} = 0,5\]
Ответ: 0,5.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.10.28 В шар массой 1,5 кг, подвешенный на нерастяжимой нити длиной 55 см, попадает
2.10.30 Тележка стоит на гладких рельсах. Человек переходит с одного её конца на другой
2.10.31 Человек массой 80 кг захотел спуститься по веревочной лестнице из свободно