Условие задачи:
К потолку лифта на нити длиной 40 см прикреплен шар массой 800 г, который вращается с частотой 90 об/мин вокруг вертикальной оси. Найти угол наклона нити к вертикали, когда лифт движется вверх с ускорением \(a=3\) м/с2.
Задача №2.4.29 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(l=40\) см, \(m=800\) г, \(\nu=90\) об/мин, \(a=3\) м/с2, \(\alpha-?\)
Решение задачи:
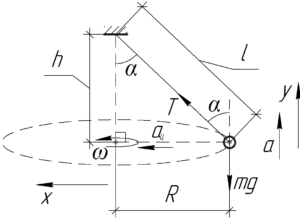 На схеме покажем шар, все силы, действующие на него и геометрические параметры задачи. Во-первых, шарик движется с ускорением \(a\) вверх вместе с лифтом, во-вторых, он движется равномерно по окружности некоторого радиуса \(R\). Запишем два раза второй закон Ньютона в проекции на оси координат:
На схеме покажем шар, все силы, действующие на него и геометрические параметры задачи. Во-первых, шарик движется с ускорением \(a\) вверх вместе с лифтом, во-вторых, он движется равномерно по окружности некоторого радиуса \(R\). Запишем два раза второй закон Ньютона в проекции на оси координат:
\[\left\{ \begin{gathered}
T \cdot \cos \alpha — mg = ma \hfill \\
T \cdot \sin \alpha = m{a_ц} \hfill \\
\end{gathered} \right.\]
Выразим центростремительное ускорение шарика \(a_ц\) через частоту вращения \(\nu\), данную в условии. Для этого нам необходимы следующие две формулы:
\[{a_ц} = {\omega ^2}R\]
\[\omega = 2\pi \nu \]
Таким образом, получим такую формулу:
\[{a_ц} = 4{\pi ^2}{\nu ^2}R\]
Если подставить полученное выражение во второе равенство системы, а первое переписать в другом виде, то получим:
\[\left\{ \begin{gathered}
T \cdot \cos \alpha = m\left( {a + g} \right) \hfill \\
T \cdot \sin \alpha = 4{\pi ^2}{\nu ^2}mR \hfill \\
\end{gathered} \right.\]
Поделим нижнее равенство на верхнее, тогда:
\[tg\alpha = \frac{{4{\pi ^2}{\nu ^2}R}}{{a + g}}\]
Теперь обратимся к схеме. Очевидно, что:
\[tg\alpha = \frac{R}{h} = \frac{R}{{l \cdot \cos \alpha }}\]
\[\frac{R}{{l \cdot \cos \alpha }} = \frac{{4{\pi ^2}{\nu ^2}R}}{{a + g}}\]
\[\frac{1}{{l \cdot \cos \alpha }} = \frac{{4{\pi ^2}{\nu ^2}}}{{a + g}}\]
\[\alpha = \arccos \left( {\frac{{a + g}}{{4{\pi ^2}{\nu ^2}l}}} \right)\]
Переведем длину нити и частоту вращения в единицы системы СИ.
\[40\; см = \frac{{40}}{{100}}\; м = 0,4\; м\]
\[90\; об/мин = \frac{{90}}{{60}}\; Гц = 1,5\; Гц\]
Теперь посчитаем ответ:
\[\alpha = \arccos \left( {\frac{{3 + 10}}{{4 \cdot {{3,14}^2} \cdot {{1,5}^2} \cdot 0,4}}} \right) = 68,5^\circ \]
Обратите внимание, что угол наклона нити не зависит от массы шарика.
Ответ: 68,5°.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.4.28 Тело массой 4 кг вращают в вертикальной плоскости с помощью резинового шнура
2.4.30 Какова должна быть максимальная длина выпуклого симметричного относительно
2.4.31 Маленький шарик, подвешенный на нити, движется по окружности так, что нить
примерно 17.5 градусов
Огромное спасибо за решение! Очень помогли
как вы полученный ответ (у меня он 0,37) перевели в градусы?
Если режим представления угловых величин в калькуляторе выставлен на DEG (degrees — градусы), то когда вы считаете arccos, он Вам сразу должен ответ выдавать в градусах.
Но если Вы каким то образом получили ответ в радианах, а Вам нужно перевести в градусы, то полученное число Вы делите на 3,14 и умножаете на 180 — полученное в результате число будет углом, выраженным в градусах.
По-моему, после этого переписку можно тоже удалить, так как это не очень мысли.. В том смысле, что мало кому интересны после того как всё исправлено.
«Для этого нам необходимы следующие две формулЫ:»
Исправил