Условие задачи:
Груз, подвешенный на нити длиной 98 см, равномерно вращается по окружности в горизонтальной плоскости. Найти угловую скорость вращения груза, если при его вращении нить отклонена от вертикали на угол 60°? (\(g=9,8\) м/с2)
Задача №2.4.19 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(l=98\) см, \(\alpha=60^\circ\), \(g=9,8\) м/с2, \(\omega-?\)
Решение задачи:
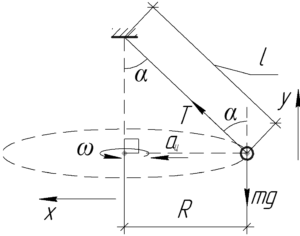 На схеме покажем груз, действующие на него силы и геометрические параметры задачи. Груз покоится относительно оси \(y\), что дает нам право применить первый закон Ньютона в проекции на ось \(y\):
На схеме покажем груз, действующие на него силы и геометрические параметры задачи. Груз покоится относительно оси \(y\), что дает нам право применить первый закон Ньютона в проекции на ось \(y\):
\[T \cdot \cos \alpha = mg\;\;\;\;(1)\]
Так как груз в горизонтальной плоскости равномерно движется по окружности некоторого радиуса \(R\), то запишем второй закон Ньютона в проекции на ось \(x\):
\[T \cdot \sin \alpha = m{a_ц}\]
Поскольку нам нужно найти угловую скорость вращения \(\omega\), то запишем такую формулу определения ускорения \(a_ц\):
\[{a_ц} = {\omega ^2}R\]
\[T \cdot \sin \alpha = m{\omega ^2}R\;\;\;\;(2)\]
Поделим полученное равенство (2) на равенство (1):
\[tg\alpha = \frac{{{\omega ^2}R}}{g}\]
Из прямоугольного треугольника с катетом \(R\), гипотенузой \(l\) и углом \(\alpha\) верно, что:
\[R = l \cdot \sin \alpha \]
Тогда:
\[tg\alpha = \frac{{{\omega ^2}l \cdot \sin \alpha }}{g}\]
\[\frac{1}{{\cos \alpha }} = \frac{{{\omega ^2}l}}{g}\]
\[\omega = \sqrt {\frac{g}{{l \cdot \cos \alpha }}} \]
Переведем длину нити в единицы системы СИ, далее посчитаем численный ответ задачи.
\[98\; см = \frac{{98}}{{100}}\; м = 0,98\; м\]
\[\omega = \sqrt {\frac{{9,8}}{{0,98 \cdot \cos 60^\circ }}} = 4,5\; рад/с\]
Ответ: 4,5 рад/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.4.18 Груз, подвешенный на нити длиной 5 м, равномерно движется по окружности
2.4.20 Лыжник съезжает с вершины горы. На какой высоте от начала движения его давление
2.4.21 Люстра массой 10 кг висит на цепи, прочность которой 196 Н. На какой максимальный угол