Условие задачи:
Груз, подвешенный на нити длиной 5 м, равномерно движется по окружности в горизонтальной плоскости. Найти период вращения груза, если при его движении нить отклонена от вертикали на угол 60°.
Задача №2.4.18 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(l=5\) м, \(\alpha=60^\circ\), \(T-?\)
Решение задачи:
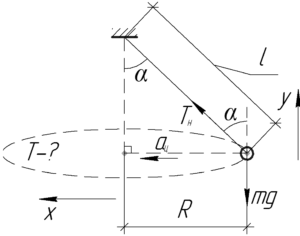 На схеме покажем груз, подвешенный на нити и движущийся по окружности некого радиуса \(R\) в горизонтальной плоскости так, что нить составляет с вертикалью угол \(\alpha\). На груз действуют две силы: сила тяжести \(mg\) и сила натяжения нити \(T_н\). Так как груз не движется вдоль оси \(y\), то запишем первый закон Ньютона в проекции на эту ось:
На схеме покажем груз, подвешенный на нити и движущийся по окружности некого радиуса \(R\) в горизонтальной плоскости так, что нить составляет с вертикалью угол \(\alpha\). На груз действуют две силы: сила тяжести \(mg\) и сила натяжения нити \(T_н\). Так как груз не движется вдоль оси \(y\), то запишем первый закон Ньютона в проекции на эту ось:
\[{T_н} \cdot \cos \alpha = mg\;\;\;\;(1)\]
Поскольку груз описывается окружность, то второй закон Ньютона в проекции на ось \(y\) запишется так:
\[{T_н} \cdot \sin \alpha = m{a_ц}\;\;\;\;(2)\]
Понятно, что искомый период \(T\) содержится в ускорении \(a_ц\). Поэтому запишем две формулы: формулу определения центростремительного ускорения через угловую скорость \(\omega\) и формулу связи последней с периодом вращения.
\[{a_ц} = {\omega ^2}R\]
\[\omega = \frac{{2\pi }}{T}\]
Подставив нижнее выражение в верхнюю формулу, получим:
\[{a_ц} = \frac{{4{\pi ^2}}}{{{T^2}}}R\]
С учетом последнего, равенство (2) примет вид:
\[{T_н} \cdot \sin \alpha = \frac{{4{\pi ^2}}}{{{T^2}}}mR\]
Полученное поделим на равенство (1), тогда:
\[tg\alpha = \frac{{4{\pi ^2}R}}{{g{T^2}}}\]
\[T = 2\pi \sqrt {\frac{R}{{g \cdot tg\alpha }}} \]
На схеме прекрасно видно, что имеет место такое равенство:
\[R = l \cdot \sin \alpha \]
\[T = 2\pi \sqrt {\frac{{l \cdot \sin \alpha }}{{g \cdot tg\alpha }}} \]
\[T = 2\pi \sqrt {\frac{{l \cdot \cos \alpha }}{g}} \]
Осталось последнее действие — посчитать ответ.
\[T = 2 \cdot 3,14\sqrt {\frac{{5 \cdot \cos 60^\circ }}{{10}}} = 3,14\; с\]
Ответ: 3,14 с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.4.17 Груз массой 1 кг, привязанный к нити, отклоняют на 90 градусов от положения
2.4.19 Груз, подвешенный на нити длиной 98 см, равномерно вращается по окружности
2.4.20 Лыжник съезжает с вершины горы. На какой высоте от начала движения его давление
Tн * sin α=m * aц
Почему не Tн * sin α= — m * a ц (проблема в знаке)
А откуда появляется минус? Посмотрите на рисунке, куда я направил ось \(x\), а также куда у меня направлены сила натяжения \(T_{н}\) и центростремительное ускорение \(a_{ц}\)
Вы уверены, что правильно решили эту задачу? Допустим, что угол α равен 90°, то есть имеем крайний случай конического маятника, когда шарик вместе с нитью вращается в горизонтальной плоскости. В этом случае проекция силы натяжения нити Tн на ось y равна нулю. Тогда какая сила уравновешивает силу тяжести mg? Похоже, Вы что-то упустили.
Для текущих исходных данных, приведенных в условии, задача решена верно.
Для случая \(\alpha=90^\circ\) должна присутствовать некоторая сила, которая будет уравновешивать силу тяжести. Например, вращение груза должно происходить на плоскости.