Условие задачи:
Груз массой 4 кг подвешен на пружине жесткостью 1 кН/м. Определите дополнительную деформацию пружины, если она подвешена вместе с грузом к потолку лифта, движущегося вверх с ускорением 3 м/с2.
Задача №2.6.13 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=4\) кг, \(k=1\) кН/м, \(a=3\) м/с2, \(\Delta x-?\)
Решение задачи:
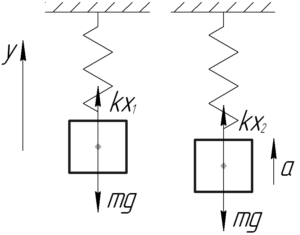В состоянии равновесия пружина растянута на некоторую величину \(x_1\), которую можно определить, записав первый закон Ньютона:
\[mg = k{x_1}\]
\[{x_1} = \frac{{mg}}{k}\]
Движущийся с ускорением лифт не является инерциальной системой отсчета, поэтому будет рассматривать груз относительно Земли. Применим второй закон Ньютона в проекции на ось \(y\):
\[k{x_2} – mg = ma\]
\[{x_2} = \frac{{ma}}{k} + \frac{{mg}}{k}\]
Очевидно, что искомую дополнительную деформацию можно найти по формуле:
\[\Delta x = {x_2} – {x_1}\]
\[\Delta x = \frac{{ma}}{k} + \frac{{mg}}{k} – \frac{{mg}}{k}\]
\[\Delta x = \frac{{ma}}{k}\]
Задача решена, остается только произвести расчет численного ответа.
\[\Delta x = \frac{{4 \cdot 3}}{{1000}} = 0,012\;м\]
Ответ: 0,012 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.6.12 К резинке длиной 50 см привязана гирька массой 20 г. При вращении гирьки
2.6.14 Какую минимальную работу необходимо совершить, чтобы передвинуть по
2.6.15 Деревянный брусок массы 2 кг тянут равномерно по горизонтальной доске с помощью