Условие задачи:

Груз массой 0,5 кг падает с некоторой высоты на плиту массой 1 кг, укрепленную на пружине с коэффициентом жесткости 10³ Н/м. Определите величину наибольшего сжатия пружины, если в момент неупругого удара груз обладал скоростью 5 м/с. Время удара ничтожно мало.

Задача №2.10.8 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=0,5\) кг, \(M=1\) кг, \(k=10^3\) Н/м, \(\upsilon_0=5\) м/с, \(x-?\)

Решение задачи:

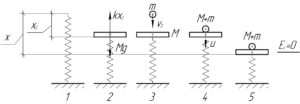Перед нами очень интересная задача, которую выполнить правильно могут лишь единицы. Начнем с самого простого: допустив, что удар груза о плиту очень быстрый, запишем закон сохранения импульса для этого момента (смотри 3 и 4 на рисунке):

\[m{\upsilon _0} = \left( {M + m} \right)u\]

\[u = \frac{{m{\upsilon _0}}}{{M + m}}\;\;\;\;(1)\]

Далее, конечно же, запишем закон сохранения энергии (после неупругого удара, чтобы не учитывать тепло). Тут многие начинают ошибаться, и первая ошибка заключается в том, что многие думают, что пружина изначально недеформирована, хотя это не так (смотри 1 и 2 на рисунке). Запишем первый закон Ньютона для плиты и пружины, откуда и узнаем начальную деформацию пружины \(x_0\):

\[Mg = k{x_0}\]

\[{x_0} = \frac{{Mg}}{k}\;\;\;\;(2)\]

Вторая ошибка — почему-то решающие забывают про изменение потенциальной энергии тел в поле тяжести. С учётом всего сказанного, запишем ЗСЭ:

\[\frac{{\left( {M + m} \right){u^2}}}{2} + \frac{{kx_0^2}}{2} + \left( {M + m} \right)g\left( {x — {x_0}} \right) = \frac{{k{x^2}}}{2}\]

Учитывая (1) и (2), получим:

\[\frac{{\left( {M + m} \right)}}{2} \cdot \frac{{{m^2}\upsilon _0^2}}{{{{\left( {M + m} \right)}^2}}} + \frac{k}{2} \cdot \frac{{{M^2}{g^2}}}{{{k^2}}} + \left( {M + m} \right)gx — \left( {M + m} \right)g{x_0} = \frac{{k{x^2}}}{2}\]

\[\frac{{{m^2}\upsilon _0^2}}{{2\left( {M + m} \right)}} + \frac{{{M^2}{g^2}}}{{2k}} + \left( {M + m} \right)gx — \frac{{\left( {M + m} \right)M{g^2}}}{k} = \frac{{k{x^2}}}{2}\]

\[\frac{{k{x^2}}}{2} — \left( {M + m} \right)gx + \frac{{\left( {M + m} \right)M{g^2}}}{k} — \frac{{{M^2}{g^2}}}{{2k}} — \frac{{{m^2}\upsilon _0^2}}{{2\left( {M + m} \right)}} = 0\]

Видно, что мы получили квадратное уравнение относительно \(x\). Чтобы решить его, найдем дискриминант \(D\).

\[D = {\left( {M + m} \right)^2}{g^2} — 4 \cdot \frac{k}{2}\left( {\frac{{\left( {M + m} \right)M{g^2}}}{k} — \frac{{{M^2}{g^2}}}{{2k}} — \frac{{{m^2}\upsilon _0^2}}{{2\left( {M + m} \right)}}} \right)\]

Распишем квадрат суммы:

\[D = {M^2}{g^2} + 2mM{g^2} + {m^2}{g^2} — 2k\left( {\frac{{{M^2}{g^2}}}{k} + \frac{{mM{g^2}}}{k} — \frac{{{M^2}{g^2}}}{{2k}} — \frac{{{m^2}\upsilon _0^2}}{{2\left( {M + m} \right)}}} \right)\]

Раскроем скобки:

\[D = {M^2}{g^2} + 2mM{g^2} + {m^2}{g^2} — 2{M^2}{g^2} — 2mM{g^2} + {M^2}{g^2} + \frac{{{m^2}\upsilon _0^2k}}{{\left( {M + m} \right)}}\]

\[D = {m^2}{g^2} + \frac{{{m^2}\upsilon _0^2k}}{{\left( {M + m} \right)}}\]

Тогда:

\[x = \frac{{\left( {M + m} \right)g \pm m\sqrt {{g^2} + \frac{{\upsilon _0^2k}}{{\left( {M + m} \right)}}} }}{k}\]

\[x = \frac{{\left( {M + m} \right)g}}{k} \pm \frac{m}{k}\sqrt {{g^2} + \frac{{\upsilon _0^2k}}{{\left( {M + m} \right)}}} \]

Посчитаем ответ:

\[x = \frac{{\left( {1 + 0,5} \right) \cdot 10}}{{{{10}^3}}} \pm \frac{{0,5}}{{{{10}^3}}}\sqrt {{{10}^2} + \frac{{{5^2} \cdot {{10}^3}}}{{\left( {1 + 0,5} \right)}}} \]

\[\left[ \begin{gathered}
x = 0,08 \; м = 8 \; см \hfill \\
x = — 0,05 \; м\hfill \\
\end{gathered} \right.\]

Понятно, что второй корень не может быть решением этой задачи.

Представленное решение неоптимально: если решать с учетом того, что после удара будет происходить колебательный процесс, то в задаче можно было обойтись без решения квадратного уравнения, а только математическими преобразованиями. Да и члены итоговой формулы приобрели бы некий смысл.

Ответ: 8 см.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.10.7 Охотник стреляет с легкой надувной лодки, находящейся в покое. Какую скорость
2.10.9 Масса пушки 800 кг. Пушка выстреливает ядро массой 10 кг с начальной скоростью
2.10.10 На вагонетку массой 800 кг, катящуюся по горизонтальным рельсам со скоростью