Условие задачи:
Горизонтально расположенный диск равномерно вращается вокруг вертикальной оси с частотой 0,5 с-1. На расстоянии 0,2 м от оси вращения на диске лежит тело. Каков должен быть коэффициент трения между телом и диском, чтобы тело не скользило во время вращения диска?
Задача №2.4.6 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\nu=0,5\) с-1, \(R=0,2\) м, \(\mu-?\)
Решение задачи:
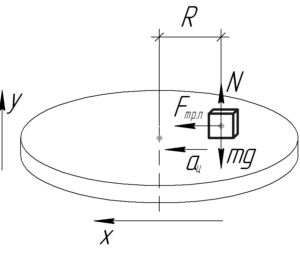На тело, находящееся на равномерно вращающемся диске, действуют 3 силы: сила тяжести, сила реакции опоры и сила трения. Причем последняя, если тело покоится относительно диска, является силой трения покоя. В задаче рассмотрим тот предельный случай, когда сила трения покоя принимает максимальное значение, т.е. когда она уже равна силе трения скольжения, но проскальзывания ещё нет.
Запишем второй закон Ньютона в проекции на ось \(x\):
\[{F_{тр.п}} = m{a_ц}\;\;\;\;(1)\]
Учитывая все написанное в первом абзаце, сила трения покоя равна:
\[{F_{тр.п}} = \mu N\]
Из первого закона Ньютона в проекции на ось \(y\) следует, что:
\[N = mg\]
Тогда максимальная сила трения покоя равна:
\[{F_{тр.п}} = \mu mg\;\;\;\;(2)\]
Центростремительное ускорение найдем из такой формулы с использованием угловой скорости вращения \(\omega\):
\[{a_ц} = {\omega ^2}R\]
Также запишем формулу связи угловой скорости и частоты вращения:
\[\omega = 2\pi \nu \]
Тогда:
\[{a_ц} = 4{\pi ^2}{\nu ^2}R\;\;\;\;(3)\]
Подставим выражения (2) и (3) в равенство (1), получим:
\[\mu mg = 4{\pi ^2}{\nu ^2}mR\]
Искомый коэффициент трения \(\mu\) равен:
\[\mu = \frac{{4{\pi ^2}{\nu ^2}R}}{g}\]
Осталось только посчитать ответ:
\[\mu = \frac{{4 \cdot {{3,14}^2} \cdot {{0,5}^2} \cdot 0,2}}{{10}} = 0,2\]
Ответ: 0,2.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.4.5 Гиря массой 100 г равномерно вращается на нити в вертикальной плоскости
2.4.7 Диск вращается с частотой 70 об/мин. На каком расстоянии от оси вращения можно
2.4.8 На горизонтальной вращающейся платформе на расстоянии 1,15 м от её вертикальной
А почему Fтр соонаправлена с F центростремительной?
Сила трения покоя \(F_{тр.п}\) направлена обратно направлению возможного движения (тело стремится вылететь с диска, как Вы понимаете). Центростремительное ускорение \(a_{ц}\) направлено к центру окружности, вокруг которого вращается тело (и диск). Так и получается, что центростремительное ускорение сонаправлено с силой трения покоя.
Да и вообще, они должны быть сонаправлены по второму закону Ньютона:\[\overrightarrow {{F_{тр.п}}} = m\overrightarrow {{a_ц}} \]
Спросили то какой-нибудь коэффициент трения при котором тело не скользит.
Можно не решать, а взять его побольше. 
Формально отвечающий будет прав. Хотя на самом деле, конечно, интересен минимальный.
Тьфу, точно. Вы правы)
«Каков должен быть МИНИМАЛЬНЫЙ коэффициент трения…» ?
При любом коэффициенте трения > 0,2 тело не будет скользить.
Заметим, что, в принципе, даже нет запрета на коэффициент трения > 1. Какой-нибудь клей или что-то вроде застёжки-липучки.
Ну я и нашёл минимальный коэффициент трения.
Если бы спрашивали про все значения коэффициента трения, при котором тело не скользит, тогда бы в формуле (2) вместо знака равно, я бы поставил меньше или равно и получил бы ответ μ>=0,2.
Про остальное сказано верно.