Условие задачи:
Два соприкасающихся бруска лежат на горизонтальном столе, по которому они могут скользить без трения. Масса первого бруска 2 кг, второго – 3 кг. Один из брусков толкают с силой 10 Н. Определить силу, с которой бруски давят друг на друга, если сила приложена к первому бруску.
Задача №2.1.70 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m_1=2\) кг, \(m_2=3\) кг, \(F=10\) Н, \(N-?\)
Решение задачи:
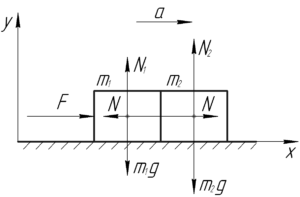На схеме к задаче нарисуем два бруска и все действующие на них силы.
На первый брусок вдоль оси \(x\) действует внешняя сила \(F\) и сила \(N\) со стороны второго бруска. На второй брусок действует только одна сила – сила \(N\) со стороны первого бруска.
Силы, действующие вдоль оси \(y\), нас не интересуют.
Понятно, что бруски при приложении внешней силы \(F\) будут двигаться с одинаковым ускорением \(a\). Запишем второй закон Ньютона для обоих брусков в проекции на ось \(x\).
\[\left\{ \begin{gathered}
F – N = {m_1}a \;\;\;\;(1)\hfill \\
N = {m_2}a \;\;\;\;(2)\hfill \\
\end{gathered} \right.\]
Сложим вместе выражения (1) и (2) системы, а из получившейся формулы выразим ускорение \(a\).
\[F = \left( {{m_1} + {m_2}} \right)a \Rightarrow a = \frac{F}{{{m_1} + {m_2}}}\]
Подставим полученную формулу для ускорения в выражение (2) системы.
\[N = \frac{{F{m_2}}}{{{m_1} + {m_2}}}\]
Посчитаем ответ:
\[N = \frac{{10 \cdot 3}}{{2 + 3}} = 6\; Н\]
Ответ: 6 Н.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.1.69 Хоккейная шайба, имея начальную скорость 5 м/с, скользит до удара о борт площадки
2.1.71 Есть два способа закинуть льдинку: бросить её под углом 45 градусов к горизонту или
2.1.72 К вертикальной стенке с силой 40 Н, направленной горизонтально, прижимается брусок
Добрый день.Помогите решить
На горизонтальной плоской поверхности расположены два соприкасающихся бруска
с массами = 1 m 2 кг и = 2 m 3 кг. Второй брусок толкают с силой
= 0F 10 Н (рисунок). Найти силу, с которой бруски давят друг на
друга, если коэффициент трения между первым бруском и
плоскостью 0,1, а между вторым бруском и плоскостью
0,2.
Ваша задача решается практически таким же образом, разве что в Вашем случае появляются силы трения скольжения. Доказывать, что сила \(F\) заставит ускоренно двигаться бруски, я не буду (если интересно – Вам нужно сравнить силу \(F\) и сумму максимальных сил трения покоя, которые действуют на каждый брусок). Итак, запишем для каждого груза второй закон Ньютона в проекции на горизонтальную ось:\[\left\{ \begin{gathered}
F – N – {F_{тр2}} = {m_2}a \hfill \\
N – {F_{тр1}} = {m_1}a \;\;\;\;(1)\hfill \\
\end{gathered} \right.\]Чтобы найти ускорение, сложим оба этих уравнения:\[F – {F_{тр1}} – {F_{тр2}} = \left( {{m_1} + {m_2}} \right)a\]Распишем силы трения скольжения:\[F – {\mu _1}{m_1}g – {\mu _2}{m_2}g = \left( {{m_1} + {m_2}} \right)a\]\[a = \frac{{F – {\mu _1}{m_1}g – {\mu _2}{m_2}g}}{{{m_1} + {m_2}}}\]Силу взаимодействия между брусками проще всего найти из уравнения (1):\[N = {m_1}a + {F_{тр1}}\]Тогда:\[N = {m_1}\frac{{F – {\mu _1}{m_1}g – {\mu _2}{m_2}g}}{{{m_1} + {m_2}}} + {\mu _1}{m_1}g\]\[N = \frac{{F{m_1} – {\mu _1}m_1^2g – {\mu _2}{m_1}{m_2}g}}{{{m_1} + {m_2}}} + \frac{{{\mu _1}{m_1}g\left( {{m_1} + {m_2}} \right)}}{{{m_1} + {m_2}}}\]\[N = \frac{{F{m_1} – {\mu _1}m_1^2g – {\mu _2}{m_1}{m_2}g + {\mu _1}m_1^2g + {\mu _1}{m_1}{m_2}g}}{{{m_1} + {m_2}}}\]\[N = \frac{{F{m_1} – \left( {{\mu _2} – {\mu _1}} \right){m_1}{m_2}g}}{{{m_1} + {m_2}}}\]Определим численный ответ:\[N = \frac{{10 \cdot 2 – \left( {0,2 – 0,1} \right) \cdot 2 \cdot 3 \cdot 10}}{{2 + 3}} = 2,8\;Н\]
Здравствуйте, а если у нас будет 3 бруска, то получается, что сила реакции третьего бруска будет направлена ко второму бруску и, записывая уравнение, мы получаем m3a = -N, но по идеи он должен тоже двигаться вправо, и получается вопрос – какая ещё на него будет действовать сила?
Зараннее спасибо за ответ.
Если Вы третий груз поставите справа от двух, изображенных на рисунке, то со стороны второго груза на него будет действовать сила \(N_1\), направленная вправо, которая и заставляет его двигаться вправо.
izvinite kopirovanni tekst iz uslovii ne otpravilos.
ia xotel popravit v tekste na brusok 2kg .
kak vi sChitaite?
bolshim uvajeniem.
gocha
Не совсем понял, зачем понадобилось это исправление