Условие задачи:
Два шарика движутся навстречу друг другу со скоростями 1 и 0,5 м/с. После удара шарики движутся в противоположные стороны со скоростями 0,5 и 1,5 м/с. Найти массу второго шарика, если масса первого равна 1 кг.
Задача №2.8.12 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_1=1\) м/с, \(\upsilon_2=0,5\) м/с, \(u_1=0,5\) м/с, \(u_2=1,5\) м/с, \(m_1=1\) кг, \(m_2-?\)
Решение задачи:
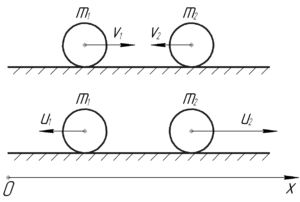 На схеме изображены данные два шарика и их скорости до и после удара. Для момента непосредственно перед ударом и сразу после него запишем закон сохранения импульса (ЗСИ) в проекции на ось \(x\):
На схеме изображены данные два шарика и их скорости до и после удара. Для момента непосредственно перед ударом и сразу после него запишем закон сохранения импульса (ЗСИ) в проекции на ось \(x\):
\[{m_1}{\upsilon _1} — {m_2}{\upsilon _2} = — {m_1}{u_1} + {m_2}{u_2}\]
В этом уравнении одно известное — искомая нами масса второго шарика \(m_2\). Перенесем все члены с множителем \(m_2\) в левую сторону, а с \(m_1\) — в правую, вынесем \(m_1\) и \(m_2\) за скобки и выразим \(m_2\).
\[{m_2}\left( {{u_2} + {\upsilon _2}} \right) = {m_1}\left( {{\upsilon _1} + {u_1}} \right)\]
\[{m_2} = \frac{{{m_1}\left( {{\upsilon _1} + {u_1}} \right)}}{{{u_2} + {\upsilon _2}}}\]
Так как все численные величины представлены в системе СИ, то можно сразу приступить к вычислению ответа.
\[{m_2} = \frac{{1 \cdot \left( {1 + 0,5} \right)}}{{1,5 + 0,5}} = 0,75\; кг = 750\; г\]
Казалось бы, всё отлично, ответ задачи найден. Но мы не заметили уловки составителя задачи, ведь при абсолютно упругом ударе относительная скорость тел должна сохраняться, т.е. должно выполняться условие (его можно вывести, если применить законы сохранения импульса и энергии):
\[{\upsilon _1} + {\upsilon _2} = {u_1} + {u_2}\]
Легко заметить, что данное условие у нас не выполняется. Также должен выполняться закон сохранения энергии (ЗСЭ):
\[\frac{{{m_1}\upsilon _1^2}}{2} + \frac{{{m_2}\upsilon _2^2}}{2} = \frac{{{m_1}u_1^2}}{2} + \frac{{{m_2}u_2^2}}{2}\]
\[\frac{{1 \cdot {1^2}}}{2} + \frac{{0,75 \cdot {{0,5}^2}}}{2} = \frac{{1 \cdot {{0,5}^2}}}{2} + \frac{{0,75 \cdot {{1,5}^2}}}{2}\]
\[0,59375\;Дж \ne 0,96875\;Дж\]
Получается, что энергия системы увеличилась, но даже при абсолютно упругом ударе она должна была просто не измениться.
При всей простоте подобных задач всегда следует проявлять бдительность и не ограничиваться одним только ЗСИ (а использовать также и ЗСЭ, если такое возможно).
Ответ: при данных условиях задача не имеет решения.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.8.11 Во сколько раз изменится потенциальная энергия пружины при увеличении
2.8.13 Камень массой 2 кг брошен вертикально вверх, его начальная кинетическая энергия
2.8.14 Маленький шарик массой m, закрепленный на нерастяжимой нити в поле силы
Странная задачка!?!
1) коэффициент восстановления Ньютона больше 1 (отношение относительных скоростей после удара к относительной скорости до удара)…
т.е. во время удара добавили энергию… каким-то образом…
2)
Посчитаем энергию до удара: 0,59375 Дж
Посчитаем энергию после удара: 0,96875 Дж
Странненько…
3) Во время удара энергия либо остается прежней (абсолютно упругий удар), либо теряется: |k| < 1
Огромнейшее спасибо за ценнейший комментарий, премного Вам благодарен!
Решение задачи откорректировано и дополнено!
Помогите пожалуйста решить задачу:
Пластилиновый шарик массой 200 г движется навстречу свинцовому массой 100 г. Определить их скорость после неупругого удара, если скорость пластилинового 2 м/с, а скорость свинцового 4 м/с.
Напишите в группе в ВК