Условие задачи:

Диск вращается с частотой 70 об/мин. На каком расстоянии от оси вращения можно положить на диск небольшое тело, чтобы оно не соскользнуло? Коэффициент трения покоя о диск $\mu=0,44$.

Задача №2.4.7 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$\nu=70$ об/мин, $\mu=0,44$, $R-?$

Решение задачи:

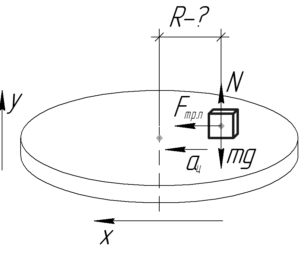Тело не соскальзывает с диска, если между ним и диском действует сила трения покоя. Максимальная её величина определяется по формуле:

$${F_{тр.п}} = \mu N$$

Из первого закона Ньютона в проекции на ось $y$ следует, что:

$$N = mg$$

$${F_{тр.п}} = \mu mg\;\;\;\;(1)$$

Запишем второй закон Ньютона в проекции на ось $x$:

$${F_{тр.п}} = m{a_ц}\;\;\;\;(2)$$

Запишем формулу определения центростремительного ускорения через угловую скорость и формулу связи последней с частотой вращения:

$${a_ц} = {\omega ^2}R$$

$$\omega  = 2\pi \nu$$

Объединив обе формулы, имеем:

$${a_ц} = 4{\pi ^2}{\nu ^2}R\;\;\;\;(3)$$

Подставим выражения (1) и (3) в равенство (2):

$$\mu mg = 4{\pi ^2}{\nu ^2}mR$$

Выразим нужное нам расстояние $R$:

$$R = \frac{{\mu g}}{{4{\pi ^2}{\nu ^2}}}$$

Переведем значение частоты вращения в систему СИ:

$$70\; об/мин = \frac{{70}}{{60}}\; Гц = \frac{7}{6}\; Гц$$

Только теперь подставляем данные в формулу и считаем ответ:

$$R = \frac{{0,44 \cdot 10 \cdot {6^2}}}{{4 \cdot {{3,14}^2} \cdot {7^2}}} = 0,082\; м$$

Ответ: 0,082 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.4.6 Горизонтально расположенный диск равномерно вращается вокруг вертикальной оси
2.4.8 На горизонтальной вращающейся платформе на расстоянии 1,15 м от её вертикальной
2.4.9 Определить силу, действующую на летчика, выводящего самолет из пикирования