Условие задачи:
Чтобы на неподвижном блоке поднимать равномерно груз, требуется усилие 270 Н, а чтобы опускать — 250 Н. Чему равна масса груза?
Задача №2.1.56 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
F1=270 Н, F2=250 Н, m−?
Решение задачи:
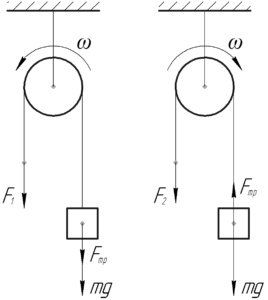Различие в усилиях при подъеме и опускании груза связано с наличием силы трения между нитью и блоком.
Если груз движется равномерно, то и блок вращается равномерно (без углового ускорения). В этом случае сумма моментов всех сил должна быть равна нулю.
Напомним, что моментом силы называется произведение силы на плечо. Плечо — это кратчайшее расстояние от точки (оси блока) до линии действия силы. Знак перед моментом определяется тем, как вращает данный момент нужную точку — если против часовой стрелки, то знак «плюс», иначе — знак «минус».
Сила трения между нитью и блоком направлена против движения груза. На схеме сила трения приложена к грузу, хотя по факту она возникает в месте контакта нити и блока — силу можно перемещать вдоль линии её действия, поэтому здесь ошибки нет.
Для случая подъема:
{F_1} \cdot R — mg \cdot R — {F_{тр}} \cdot R = 0
{F_1} — mg — {F_{тр}} = 0\;\;\;\;(1)
Обратите внимание, что у всех сил одинаковое плечо, равное радиусу блока R. Также можно видеть, что в выражении нет никакой силы натяжения нити, так как от этой связи мы не избавлялись.
Для случая опускания:
{F_2} \cdot R — mg \cdot R + {F_{тр}} \cdot R = 0
{F_2} — mg + {F_{тр}} = 0\;\;\;\;(2)
Сложим выражения (1) и (2).
{F_1} + {F_2} — 2mg = 0
m = \frac{{{F_1} + {F_2}}}{{2g}}
Масса груза равна:
m = \frac{{270 + 250}}{{2 \cdot 10}} = 26\; кг
Ответ: 26 кг.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.1.55 Через сколько секунд тело, брошенное вертикально вверх со скоростью 44,8 м/с
2.1.57 На гладкой доске лежат два тела массами 2 и 3 кг, соединенные легкой нерастяжимой
2.1.58 Человек везет двое связанных между собой саней, прикладывая к веревке силу 120 Н
F2равно по условию задачи минус 250
Также можно видеть, что в выражении нет никакой силы натяжения нити, так как от этой связи мы не избавлялись. Что?
Задачу можно решать иным способом, «разрывая» связь в виде нити и записывать:
\left\{ \begin{gathered} {F_1} — T = 0 \hfill \\ T — mg — {F_{тр}} = 0 \hfill \\ \end{gathered} \right.
Но я в своем решении связь не разрываю, о чем и пишу, и сразу получаю:
{F_1} — mg — {F_{тр}} = 0