Условие задачи:
Через сколько секунд тело, брошенное вертикально вверх со скоростью 44,8 м/с, упало на Землю, если сила сопротивления воздуха не зависела от скорости и составляла в среднем 1/7 часть силы тяжести?
Задача №2.1.55 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_0=44,8\) м/с, \(F_{с}=\frac{1}{7}mg\), \(t-?\)
Решение задачи:
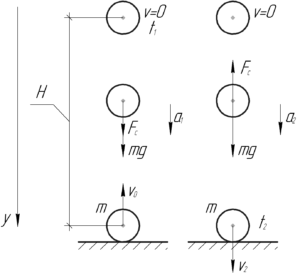 Искомое время полета \(t\) складывается из времени полета вверх \(t_1\) и времени полета вниз \(t_2\). Неверно думать, что \(t_1\) и \(t_2\) равны друг другу! Дело в том, что в этом примере имеется сила сопротивления, которая вносит свои коррективы.
Искомое время полета \(t\) складывается из времени полета вверх \(t_1\) и времени полета вниз \(t_2\). Неверно думать, что \(t_1\) и \(t_2\) равны друг другу! Дело в том, что в этом примере имеется сила сопротивления, которая вносит свои коррективы.
\[t = {t_1} + {t_2}\;\;\;\;(1)\]
Рассмотрим движение тела вверх. В этом случае сила тяжести \(mg\) и сила сопротивления \(F_{с}\) сонаправлены. Из второго закона Ньютона следует:
\[mg + {F_{с}} = ma_1\]
Так как по условию \(F_{с}=\frac{1}{7}mg\), то:
\[mg + \frac{1}{7}mg = m{a_1}\]
\[{a_1} = \frac{8}{7}g\]
Чтобы найти время \(t_1\), запишем формулу скорости для равнозамедленного движения:
\[\upsilon = {\upsilon _0} — {a_1}t\]
В наивысшей точке полета, которую тело достигнет через время \(t_1\), скорость тела равна нулю (\(\upsilon=0\)), поэтому:
\[\upsilon = 0 \Rightarrow {\upsilon _0} — {a_1}{t_1} = 0 \Rightarrow {t_1} = \frac{{{\upsilon _0}}}{{{a_1}}}\]
\[{t_1} = \frac{{7{\upsilon _0}}}{{8g}}\;\;\;\;(2)\]
Воспользуемся следующей формулой, чтобы найти высоту подъема:
\[{\upsilon ^2} — \upsilon _0^2 = — 2{a_1}H\]
\[\upsilon = 0 \Rightarrow \upsilon _0^2 = 2{a_1}H\]
\[H = \frac{{\upsilon _0^2}}{{2{a_1}}} = \frac{{7\upsilon _0^2}}{{2 \cdot 8g}} = \frac{{7\upsilon _0^2}}{{16g}}\]
Теперь рассмотрим движение тела вниз. В этом случае сила тяжести \(mg\) и сила сопротивления \(F_{с}\) противоположно направлены. Аналогично, из второго закона Ньютона следует:
\[mg — {F_с} = m{a_2}\]
\[mg — \frac{1}{7}mg = m{a_2}\]
\[{a_2} = \frac{6}{7}g\]
Тело будет падать с высоты \(H\) без начальной скорости с ускорением \(a\), поэтому верна следующая формула:
\[H = \frac{{{a_2}t_2^2}}{2}\]
Отсюда нужное нам время \(t_2\) равно:
\[{t_2} = \sqrt {\frac{{2H}}{{{a_2}}}} \]
\[{t_2} = \sqrt {\frac{{2 \cdot 7\upsilon _0^2 \cdot 7}}{{16g \cdot 6g}}} = \frac{{7{\upsilon _0}}}{{4\sqrt 3 g}}\;\;\;\;(3)\]
Формулы (2) и (3) вносим в (1):
\[t = \frac{{7{\upsilon _0}}}{{8g}} + \frac{{7{\upsilon _0}}}{{4\sqrt 3 g}} = \frac{{7{\upsilon _0}}}{{4g}}\left( {\frac{1}{2} + \frac{1}{{\sqrt 3 }}} \right)\]
Полное время полета равно:
\[t = \frac{{7 \cdot 44,8}}{{4 \cdot 10}}\left( {\frac{1}{2} + \frac{1}{{\sqrt 3 }}} \right) = 8,45\; с\]
Ответ: 8,45 с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.1.54 Троллейбус, масса которого 12 т, трогаясь с места, за 5 с проходит по горизонтальному
2.1.56 Чтобы на неподвижном блоке поднимать равномерно груз, требуется усилие 270 Н
2.1.57 На гладкой доске лежат два тела массами 2 и 3 кг, соединенные легкой нерастяжимой
в первой полученной формуле высоты скорость в квадрате, в действии, когда находится время — нет
Скорость во втором случае была в квадрате и под корнем, поэтому при извлечении корня квадрат исчез
Я не эксперт, но походу в уравнении 3 ошибка, там g не под корнем должно быть, так ведь? Или у меня голова после 30 задач кипит и я ошибаюсь?
Ошибки нет, под корнем там \(g^2\), то есть \(g\) вне корня
Понял, спасибо, казалось, что корень «заходит «на g
Зачем вы получаете такой ответ , если можно найти время по формуле равнозамедленного движения подставив
Ускорение тела будет разным при движении наверх и вниз из-за силы сопротивления воздуха, Вы это учли?