Условие задачи:
Человек, сидящий в лодке, бросает камень под углом 60° к горизонту. Масса камня 1 кг, масса человека с лодкой 150 кг, начальная скорость камня 10 м/с. Найти расстояние между точкой падения камня и лодкой в момент, когда камень коснулся воды. Трением лодки о воду пренебречь.
Задача №2.10.37 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\alpha=60^\circ\), \(m=1\) кг, \(M=150\) кг, \(\upsilon_0=10\) м/с, \(L-?\)
Решение задачи:
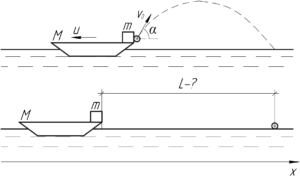После того, как человек бросит камень, лодка тоже придет в движение. Так как на систему “лодка – человек – камень” не действуют горизонтальные силы, то суммарный импульс в проекции на ось \(x\) должен сохраняться по закону сохранения импульса:
\[0 = m{\upsilon _0}\cos \alpha – Mu\]
Отсюда скорость лодки \(u\) равна:
\[u = \frac{{m{\upsilon _0}\cos \alpha }}{M}\;\;\;\;(1)\]
До падения в воду камень будет двигаться время \(2t\), где \(t\) – это время подъема камня до наивысшей точки своей траектории, равное:
\[t = \frac{{{\upsilon _0}\sin \alpha }}{g}\;\;\;\;(2)\]
За время \(2t\) лодка и камень удалять друг от друга на расстояние \(L\), которое можно найти по такой формуле:
\[L = \left( {{\upsilon _0}\cos \alpha + u} \right) \cdot 2t\]
Подставим (1) и (2) в эту формулу, тогда получим:
\[L = \left( {{\upsilon _0}\cos \alpha + \frac{{m{\upsilon _0}\cos \alpha }}{M}} \right) \cdot \frac{{2{\upsilon _0}\sin \alpha }}{g}\]
\[L = \frac{{\upsilon _0^2\sin 2\alpha }}{g}\left( {1 + \frac{m}{M}} \right)\]
Подставим исходные данные в формулу и посчитаем ответ:
\[L = \frac{{{{10}^2} \cdot \sin 120^\circ }}{{10}}\left( {1 + \frac{1}{{150}}} \right) = 8,72\; м = 872\; см\]
Ответ: 872 см.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.10.36 Снаряд, выпущенный из пушки под углом 45 градусов к горизонту, разрывается
2.1.1 Тело движется прямолинейно под действием силы 16 Н. Зависимость пути от времени
2.1.2 Тело массой 3 кг движется горизонтально с ускорением 4 м/с2. Определить