Условие задачи:
Брусок сползает без начальной скорости с высоты 2 м по доске, наклоненной под углом 45° к горизонту. После спуска брусок попадает на горизонтальный пол. Коэффициенты трения бруска о доску и пол одинаковы и равны 0,5. На каком расстоянии от конца доски остановится брусок?
Задача №2.3.12 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(H=2\) м, \(\alpha=45^\circ\), \(\mu=0,5\), \(S-?\)
Решение задачи:
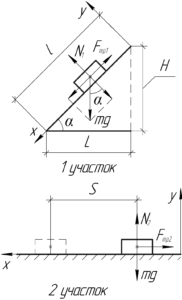Проще всего эту задачу можно решить, используя закон сохранения энергии, по которому работа неконсервативной силы (силы трения в данном случае) равна изменению полной механической энергии бруска.
\[A = \Delta E\;\;\;\;(1)\]
Когда брусок остановится, пройдя путь \(S\) по полу, его полная механическая энергия станет равной нулю, хотя в начале она была равна \(mgH\) (потенциальная энергия). Поэтому изменение энергии \(\Delta E\) равно:
\[\Delta E = 0 – mgH = – mgH\;\;\;\;(2)\]
Так как сила трения принимает разные значения на разных участках движения, то работу найдем как следующую сумму:
\[A = {A_1} + {A_2}\;\;\;\;(3)\]
Рассмотрим 1-й участок: участок движения по доске. Брусок покоится вдоль оси \(y\), поэтому согласно первому закону Ньютона верно записать следующее:
\[N_1 = mg \cdot \cos \alpha \]
Сила трения скольжения определяется по следующей известной формуле:
\[{F_{тр1}} = \mu N_1\]
\[{F_{тр1}} = \mu mg \cdot \cos \alpha \]
Эта сила совершит отрицательную работу, равную по определению:
\[{A_1} = – {F_{тр1}} \cdot l\]
\[{A_1} = – \mu mg \cdot \cos \alpha \cdot l\]
Обратите внимание, что произведение \(\left( {l \cdot \cos \alpha } \right)\) равно \(L\) (смотрите схему). Но поскольку мы не знаем значения \(L\), выразим её через угол \(\alpha\) и высоту \(H\).
\[L = l \cdot \cos \alpha = H \cdot ctg\alpha \]
Тогда работа \(A_1\) равна:
\[{A_1} = – \mu mgH \cdot ctg\alpha \;\;\;\;(4)\]
Теперь перейдём ко 2-ому участку: участку движения по полу. Аналогично определим силу реакции опоры:
\[{N_2} = mg\]
Сила трения скольжения станет больше за счёт увеличения \(N\), её можно определить по той же общей формуле:
\[{F_{ тр2}} = \mu {N_2}\]
\[{F_{тр2}} = \mu mg\]
На втором участке сила трения совершит работу \(A_2\), определяемую формулой:
\[{A_2} = – {F_{тр2}} \cdot S\]
\[{A_2} = – \mu mgS\;\;\;\;(5)\]
Соберем выражения (2), (3), (4) и (5) в (1), получим:
\[ – \mu mgH \cdot ctg\alpha – \mu mgS = – mgH\]
Сократим на \(mg\) и домножим на \(-1\), тогда:
\[\mu H \cdot ctg\alpha + \mu S = H\]
В итоге получим такое решение задачи в общем виде:
\[S = H\left( {\frac{1}{\mu } – ctg\alpha } \right)\]
Считаем ответ:
\[S = 2\left( {\frac{1}{{0,5}} – ctg45^\circ } \right) = 2\; м\]
Ответ: 2 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.3.11 Брусок массой 3 кг находится на наклонной плоскости, составляющей угол 45 градусов
2.3.13 Ледяная гора составляет с горизонтом угол 30 градусов, по ней снизу вверх пускают
2.3.14 Ледяная горка составляет с горизонтом угол 10 градусов. По ней пускают вверх камень
Добрый день. А можно ли в данной задаче, понимая, что треугольник со сторонами Н и L равнобедренный, т.к. углы у основания 45 градусов, следовательно L будет равно Н и не нужно заморачиваться с котангенсом
Разумеется можно
Здравствуйте, а можно эту задачу решить через скорость и ускорение?То есть через скорость в момент когда брусок переходит на горизонтальную поверхность? Если да, то можете написать как, буду очень признателен.
Да, можно. Не буду максимально всё расписывать, иначе тут выйдет очень много текста.
Запишем второй закон Ньютона в проекции на ось \(x\) для бруска, движущегося по наклоненной доске:
\[m{a_1} = mg\sin \alpha – \mu mg\cos \alpha \]
Откуда ускорение бруска при движении по наклоненной доске равно:
\[{a_1} = g\left( {\sin \alpha – \mu \cos \alpha } \right)\]
Аналогично запишем второй закон Ньютона в проекции на ось \(x\) для бруска, движущегося по полу:
\[m{a_2} = \mu mg\]
Откуда ускорение бруска при движении по полу равно:
\[{a_2} = \mu g\]
Воспользуемся дважды формулой кинематики без времени:
\[\left\{ \begin{gathered}
{\upsilon ^2} = 2{a_1}l \hfill \\
{\upsilon ^2} = 2{a_2}S \hfill \\
\end{gathered} \right.\]
Откуда имеем:
\[{a_1}l = {a_2}S\]
\[S = \frac{{{a_1}}}{{{a_2}}}l\]
\[S = \frac{{g\left( {\sin \alpha – \mu \cos \alpha } \right)}}{{\mu g}}l\]
\[S = \left( {\frac{1}{\mu }\sin \alpha – \cos \alpha } \right)l\]
Из прямоугольного треугольника видно, что:
\[l = \frac{H}{{\sin \alpha }}\]
Тогда:
\[S = H\left( {\frac{1}{\mu } – ctg\alpha } \right)\]
Как Вы видите, мы получили абсолютно такой же ответ.
\(L = l\cos \alpha \)
\(tg\alpha = \frac{H}{L}\) отсюда следует \(L = \frac{H}{{tg\alpha }} = Hctg\alpha \)
значит \(l\cos \alpha = Hctg\alpha \)
Разве не так?
Так, решение поправил, спасибо!
День добрый подскажите почему стоит тангенс угла?
Рассмотрите внимательно прямоугольный треугольник, который образуют пол и доска под углом α к нему.