Условие задачи:

Автомобиль при полностью включенных тормозах (колеса не вращаются) может удержаться на участке горной дороги с наклоном до 30°. Каков тормозной путь этого автомобиля на горизонтальном участке той же дороги при скорости 72 км/ч?

Задача №2.3.9 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=30^\circ\), \(\upsilon_0=72\) км/ч, \(S-?\)

Решение задачи:

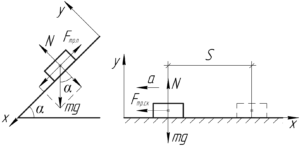Первое предложение в задаче приведено для того, чтобы мы нашли коэффициент трения. Рассмотрим этот случай (левая часть схемы). На автомобиль будут действовать 3 силы: сила тяжести, сила реакции опоры и сила трения покоя. Причем сила трения покоя уже примет максимальное значение, т.е. будет равна силе трения скольжения, но скольжение ещё не происходит.

Запишем первый закон Ньютона в проекции на ось \(x\) (смотрите схему):

\[mg \cdot \sin \alpha  = {F_{тр.п}}\;\;\;\;(1)\]

Тело также покоится в направлении оси \(y\), поэтому по первому закону Ньютона в проекции на эту ось верно записать:

\[N = mg \cdot \cos \alpha \]

Максимальная сила трения покоя равна силе трения скольжения, определяемую формулой:

\[{F_{тр.п}} = \mu N\]

\[{F_{тр.п}} = \mu mg \cdot \cos \alpha \]

Подставим полученное в (1), откуда и найдем коэффициент трения \(\mu\):

\[mg \cdot \sin \alpha  = \mu mg \cdot \cos \alpha \]

\[\mu  = tg\alpha \;\;\;\;(2)\]

Отлично, теперь рассмотрим торможение нашего автомобиля (правая часть схемы). Из второго закон Ньютона в проекции на ось \(x\) запишем:

\[{F_{тр.ск}} = ma\;\;\;\;(3)\]

Применим первый закон Ньютона в проекции на ось \(y\), так как тело вдоль этой оси не двигается:

\[N = mg\]

Силу трения скольжения найдет по формуле:

\[{F_{тр.ск}} = \mu N\]

\[{F_{тр.ск}} = \mu mg\]

Последнее полученное подставим в (3), тогда:

\[\mu mg = ma\]

\[a = \mu g\;\;\;\;(4)\]

Тело, имея в начале скорость \(\upsilon_0\), пройдет расстояние \(S\) до остановки, двигаясь равнозамедленно с ускорением \(a\). Применим следующую формулу из кинематики:

\[0 — \upsilon _0^2 =  — 2aS\]

\[S = \frac{{\upsilon _0^2}}{{2a}}\]

Подставим (2) в (4), а полученное в последнюю формулу, тогда будем иметь решение задачи в общем виде:

\[S = \frac{{\upsilon _0^2}}{{2g \cdot tg\alpha }}\]

Переведем начальную скорость автомобиля в систему СИ:

\[72\; км/ч = \frac{{72 \cdot 1000}}{{1 \cdot 3600}}\; м/с = 20\; м/с\]

Считаем ответ:

\[S = \frac{{{{20}^2}}}{{2 \cdot 10 \cdot tg30^\circ }} = 34,64\; м\]

Ответ: 34,64 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.3.8 Тело соскальзывает без начальной скорости с наклонной плоскости. Угол наклона
2.3.10 С ледяной горки высотой 3 м и длиной основания 5 м съезжают санки, которые
2.3.11 Брусок массой 3 кг находится на наклонной плоскости, составляющей угол 45 градусов