Условие задачи:

Подвешенный на нити шарик массой 0,3 кг совершает колебания в вертикальной плоскости. Когда шарик проходит положение равновесия, сила натяжения нити вдвое больше силы тяжести. Чему равна сила натяжения нити в момент наибольшего отклонения шарика?

Задача №2.4.26 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=0,3\) кг, \(T_2=2mg\), \(T_1-?\)

Решение задачи:

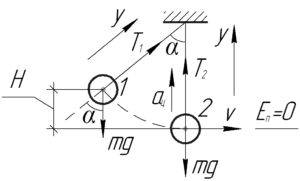В положении 1 у шарика нет скорости, значит нет и центростремительного ускорения. Поэтому первый закон Ньютона в проекции на ось \(y\) для положения 1 даст такое равенство:

\[T_1 = mg \cdot \cos \alpha \;\;\;\;(1)\]

В положении 2 у шарика уже есть некоторая скорость \(\upsilon\). Если принять, что длина нити равна \(l\), то центростремительное ускорение шарика в этой точке можно найти по формуле:

\[{a_ц} = \frac{{{\upsilon ^2}}}{l}\]

Из второго закона Ньютона в проекции на ось \(y\) (это уже другая, ещё одна введенная ось) для положения 2 следует, что:

\[{T_2} — mg = m{a_ц}\]

\[{T_2} — mg = m\frac{{{\upsilon ^2}}}{l}\]

\[{T_2} = m\left( {g + \frac{{{\upsilon ^2}}}{l}} \right)\;\;\;\;(2)\]

Чтобы найти скорость \(\upsilon\), применим закон сохранения энергии, при этом выбрав нулевой уровень потенциальной энергии на уровне положения равновесия шарика. Тогда:

\[mgH = \frac{{m{\upsilon ^2}}}{2}\]

На схеме видно, что начальная высота шарика \(H\) связана с длиной нити \(l\) и углом \(\alpha\) выражением:

\[H = l\left( {1 — \cos \alpha } \right)\]

\[mgl\left( {1 — \cos \alpha } \right) = \frac{{m{\upsilon ^2}}}{2}\]

\[{\upsilon ^2} = 2gl\left( {1 — \cos \alpha } \right)\]

Полученное выражение для квадрата скорости подставим в (2), тогда:

\[{T_2} = m\left( {g + \frac{{2gl\left( {1 — \cos \alpha } \right)}}{l}} \right)\]

\[{T_2} = mg\left( {3 — 2\cos \alpha } \right)\]

По условию \(T_2=2mg\), поэтому:

\[3 — 2\cos \alpha  = 2\]

\[\cos \alpha  = \frac{1}{2}\]

Зная косинус угла \(\alpha\), по формуле (1) можем посчитать искомое значение силы натяжения нити \(T_1\).

\[T = 0,3 \cdot 10 \cdot \frac{1}{2} = 1,5\; Н\]

Ответ: 1,5 Н.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.4.25 Поезд движется по закруглению со скоростью 50 км/ч. Шарик, подвешенный в вагоне
2.4.27 Шарик массой 200 г на нити длиной 3 м описывает в горизонтальной плоскости
2.4.28 Тело массой 4 кг вращают в вертикальной плоскости с помощью резинового шнура