Решение: На сферической планете вес тела на полюсе в 3 раза больше веса тела на экваторе

Условие задачи:

На сферической планете вес тела на полюсе в 3 раза больше веса тела на экваторе. Определите период вращения этой планеты, если её средняя плотность 2300 кг/м³.

Задача №2.5.9 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(P_п=3P_э\), \(\rho=2300\) кг/м³, \(T-?\)

Решение задачи:

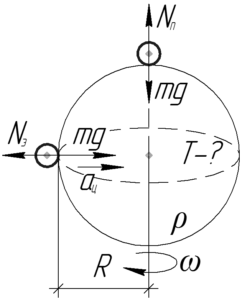Начнем с того, что вес тела равен силе реакции опоры согласно третьему закону Ньютона. Заметим, что эти силы равны по величине, противоположны по направлению и приложены к разным телам.

\[P = N\;\;\;\;(1)\]

Тело, находящееся на экваторе, вращается вместе с планетой, описывая окружность радиуса \(R\) (радиус планеты). Второй закон Ньютона для этого тела запишется в следующем виде:

\[mg — {N_э} = m{a_ц}\]

Тело на полюсе вращается вокруг своей оси, поскольку ось планеты проходит через центр масс этого тела. Так как при вращении планеты оно будет описывать окружность нулевого радиуса, значит на него не действует центростремительное ускорение. Первый закон Ньютона для этого тела будет записан в таком виде:

\[mg = {N_п}\]

Получим такую систему:

\[\left\{ \begin{gathered}
{N_э} = mg — m{a_ц} \hfill \\
{N_п} = mg \hfill \\
\end{gathered} \right.\]

Учитывая (1), имеем:

\[\left\{ \begin{gathered}
{P_э} = mg — m{a_ц} \hfill \\
{P_п} = mg \hfill \\
\end{gathered} \right.\]

Так как по условию \(P_п=3P_э\), то поделив нижнее равенство системы на верхнее, получим:

\[\frac{g}{{g — {a_ц}}} = 3\]

\[3g — 3{a_ц} = g\]

\[2g = 3{a_ц}\;\;\;\;(2)\]

Выразим ускорение свободного падения \(g\) на поверхности планеты через её среднюю плотность \(\rho\). Для этого запишем формулу его определения:

\[g = G\frac{M}{{{R^2}}}\]

Массу планеты найдем как произведение плотности на объем, а объем выразим через радиус, поскольку планета является сферической.

\[M = \rho \cdot V = \frac{4}{3}\pi \rho {R^3}\]

Тогда:

\[g = \frac{4}{3}G\frac{{\pi \rho {R^3}}}{{{R^2}}}\]

\[g = \frac{4}{3}G\pi \rho R\;\;\;\;(3)\]

Теперь выразим центростремительное ускорение \(a_ц\) через период вращения. Для этого запишем формулу определения центростремительного ускорения через угловую скорость вращения и формулу связи угловой скорости вращения с периодом обращения планеты:

\[{a_ц} = {\omega ^2}R\]

\[\omega = \frac{{2\pi }}{T}\]

Значит:

\[{a_ц} = \frac{{4{\pi ^2}}}{{{T^2}}}R\;\;\;\;(4)\]

Подставим выражения (3) и (4) в равенство (2):

\[\frac{8}{3}G\pi \rho R = \frac{{12{\pi ^2}}}{{{T^2}}}R\]

Выразим из полученного равенство период \(T\), получим решение задачи в общем виде:

\[T = 3\sqrt {\frac{\pi }{{2G\rho }}} \]

Считаем ответ:

\[T = 3\sqrt {\frac{{3,14}}{{2 \cdot 6,67 \cdot {{10}^{ — 11}} \cdot 2300}}} = 9597,2\; с \approx 160\; мин\]