Условие задачи:
Две гири неравной массы висят на концах нити, перекинутой через невесомый блок, причем легкая гиря расположена на 2 м ниже тяжелой. Если дать им возможность двигаться, то через 2 с они окажутся на одной высоте. Определите отношение массы большей гири к массе меньшей.
Задача №2.2.6 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(H=2\) м, \(t=2\) с, \(\frac{M}{m}-?\)
Решение задачи:
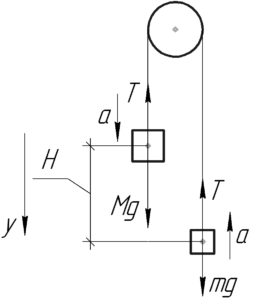Понятно, что оба тела после того, как их отпустят, начнут двигаться равноускоренно: более тяжелая гиря – вниз, другая – вверх. За время \(t\) они оба пройдут в сумме расстояние \(H\), поэтому верно записать следующее:
\[H = 2 \cdot \frac{{a{t^2}}}{2} = a{t^2}\]
Выразим ускорение гирь \(a\):
\[a = \frac{H}{{{t^2}}}\;\;\;\;(1)\]
Теперь запишем второй закон Ньютона для обоих тел в проекции на ось \(y\) (все силы показаны на схеме):
\[\left\{ \begin{gathered}
Mg – T = Ma \hfill \\
mg – T = – ma \hfill \\
\end{gathered} \right.\]
Вычтем из первого равенства второе (чтобы избавиться от неизвестной силы натяжения \(T\)):
\[Mg – mg = Ma + ma\]
Поделим обе части равенства на \(m\), чтобы найти искомое отношение \(\frac{M}{m}\):
\[\frac{M}{m}g – g = \frac{M}{m}a + a\]
\[\frac{M}{m}\left( {g – a} \right) = a + g\]
\[\frac{M}{m} = \frac{{a + g}}{{g – a}}\]
Подставим (1) в последнюю формулу, тогда получим:
\[\frac{M}{m} = \frac{{\frac{H}{{{t^2}}} + g}}{{g – \frac{H}{{{t^2}}}}}\]
\[\frac{M}{m} = \frac{{H + g{t^2}}}{{g{t^2} – H}}\]
Посчитаем ответ к этой задаче:
\[\frac{M}{m} = \frac{{2 + 10 \cdot {2^2}}}{{10 \cdot {2^2} – 2}} = 1,11\]
Ответ: 1,11.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.2.5 Два одинаковых груза массами 0,1 кг связаны между собой нитью, перекинутой
2.2.7 Через невесомый блок перекинута нерастяжимая нить, к одному из концов которой
2.2.8 К концам нерастянутой нити, перекинутой через застопоренный блок, подвешенный
а как решать эту задачу, если блок имеет массу и является сплошным диском?
При выражении ускорения через H, мы при переносе ведь должны отнимать, а не умножать .2=at^2/2 значит 0=-2+at^2/2 ?
Я не переношу, я выражаю ускорение a через H
Вы написали H=2⋅at^2\2=at^2. Но ведь общая формула H=at^2\2 почему мы домножили на 2 ?
Потому что каждая гиря пройдет до встречи путь H/2, т.е. справедливо:
H\2=at^2\2
Н=2*at^2\2
Н=at^2
Добрый день.
ответ неверный
Оба тела окажутся на одном уровне в том случае, когда каждое тело пройдет 1 метр.
То, что большей массой опустится на 1 метр, а то, что меньшей массой поднимется на 1 метр.
Только в этом случае они будут на одном уровне.
Отчего же Н равно 2 метра?
Я так и решаю, где ошибка то? У меня H – это суммарный путь, который пройдут оба груза.